Design

— Christopher R. Genovese

Plan for Today #

Design Principles and Practices
Design Example
Zipper questions?

Design Case Study: Intro #

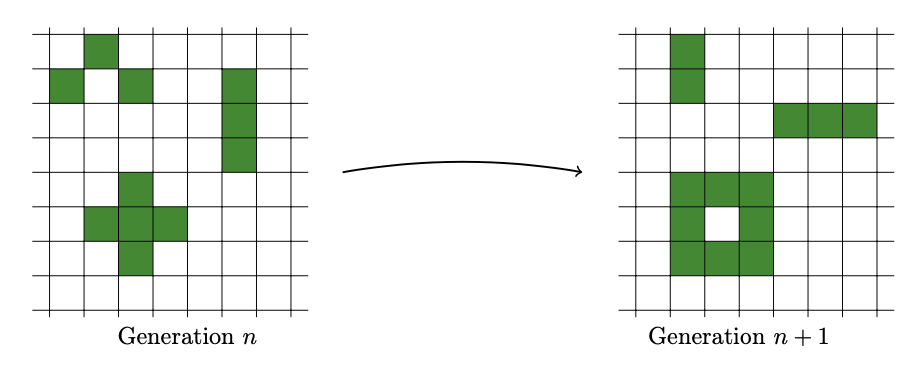
The Game of Life is a deterministic, discrete-time process devised by mathematician John Conway that is an example of what is called a cellular automaton. A cellular automaton is an arrangement cells in a grid of some shape that evolves in discrete time according to fixed rules. At any time step in the process, each cell can be in one of a finite number of states. The automaton is specified by a set of rules that describe how the state of each cell in the next time step depends on the state of the cell and its neighbors at the current time step.

In the Game of Life, the cells are the squares in an infinite, two-dimensional, regular grid in the Euclidean plane. The cells have two possible states – alive and dead – and each time step is called a generation.

Conway’s rules specify that:

A live cell lives to the next generation if and only if it has two or three live neighbors in the current generation; otherwise, it dies, by underpopulation or overcrowding.
A dead cell comes alive if and only if it has three live neighbors by reproduction; otherwise it remains dead.

The Figure below illustrates the rules.

The system admits a wide variety of interesting patterns, including patterns that oscillate and move, patterns that grow without bound, and patterns that generate other patterns at regular intervals. The Game of Life can even be with configured with patterns that simulate boolean logical operations, clock pulses, memory, and instructions – making it a programmable computer. This computer has been shown to be Turing complete, meaning that it has as much computational power as any other computer with unlimited memory and time.

Task: Design a program to simulate the Game of Life (and other cellular automata)

What are the main entities here? How do they interact?
What are the operations on those entities?
What are the main types and their laws?
What is really essential here?

Design: Philosophy, Principles, and Practices #

What do we want from our code?

Correct
Performant
Understandable
Maintianable
Easy to change and update
Easy to reuse parts for other tasks
…

Key criterion: reduce overall complexity of the system

For each of the considerations below, we will examine the issue in germs of our Game of Life example.

Sources of Complexity #

Complexity makes a system hard to understand and modify

Coupling and Change Amplification: interlocking dependencies, d/dChange is big
Cognitive Load: How much do you need to know/understand/see to complete a task
Obscurity: What don’t you know that you need to know about a system

Tactical versus Strategic Programming #

Tactical: Get it working as fast as possible – put out this fire
Strategic: Invest in a great design.

Working code is not enough!

In practice: balance required to find the right level investment

Balance in Game of Life example?

Deep versus Shallow Modules/Interfaces #

The modules in a system are the (relatively) independent pieces of functionality that comprise the system. Modules can occur at multiple scales: classes, types and laws, functions, related code organized in a file, …. A module typically represents an abstraction.

An abstraction provides a simplified view of an entity while obscuring unimportant details.

A deep module has large functionality per unit surface-area of its interface. A shallow module has relatively small functionality per unit surface area of its interface.

General purpose modules tend to be deeper than highly specialized ones and are often easier to code, test, and reuse. There is always a generality trade-off, but keep this in mind.

Example: Linux file system (Deep) #

Five basic system calls:

open: gives access to a path through a file descriptor
read: reads data from a file descriptor (at current location)
write: writes data to a file descriptor (at current location)
lseek: changes current location (only rarely needed)
close: revokes access to a file descriptor

This simple interface manages (and hides) a long list of complex tasks and decisions related to how files are stored and organized, access is scheduled, permissions recorded, information cached and buffered, and many more.

Example: Java IO #

Original steps needed to open a file in the standard way for serialized objects:

FileInputStream fileStream = new FileInputStream(FileName)
BufferedInputStream bufferedStream = new BuffferedInputStream(FileStream)
ObjectInputStream objectStream = new ObjectInputStream(bufferedStream)

Complex, verbose, common behavior is not easy or default, highly coupled.

This interface has a huge surface area relative to the functionality it provides.

Game of Life #

Information Hiding #

Each module encapsulates a few pieces of knowledge, which represent design decisions. This often consists of implmentation details or representation of information.

Information hiding serves two purposes:

Simplifies the interface
Reduces coupling and so makes it easier to change the system

Information leakage occurs when the same knowledge is used in multiple places in the code. Sometimes this is necessary to a degree, but strive to create as few dependencies as possible.

For example: if some options or defaults are only used by a subset of users, provide them with a path but don’t impinge on the typical use.

Another example: temporal coupling – steps that must be performed in order but which are separated

Each function, class, and module in your code needs some information to do its job.

Give it the information it needs but no more.

Giving too much information couples parts of the code that should be independent, making them harder to test, debug, and reason about.

Interfaces and Implementation: Modules, Layers, Abstractions #

We often organize our programs in different layers, with higher-level layers using lower-level layers.

Examples: Network protocols, File Systems

Each layer has its own abstraction, and usually the abstractions from different layers should be different.

Example: interface for a text-editor

What are the modules, layers, abstractions in GoL?

Parse Don’t Validate #

Push complexity downward
Don’t pass the buck

Consider head : List a -> a. What to do with an empty list? Raise an error?

Validating means checking that the list we pass to head is non-empty before we call it. This introduces extra checks and potential bugs.

Instead, define head : NonEmptyList a -> a for a type NonEmpty a. To create an object of type NonEmpty a you need at least one a. The exceptional conditional is not possible and applying head requires “parsing” an input value.
parsing is preferable to validation

What’s the difference? The information the steps return.
Control the boundaries of your application

Embedded Design Principle #

The code should reflect the design and intention.

Simple Example:

def logging(message, *args):
    print(message.format(*args))

More complicated example here.

Keep the contract clear Each function or class has an explicit contract behind it. “I give you this, you give me that.” Make that contract salient in your code, your tests, and your documentation.

Make Illegal States Unrepresentable #

Example: head : List a -> a and head : NonEmpty a -> a again.

We can also use this to define errors away.

Example: substring(s, start, end) – what to do if start or end is out of range?

Example: unset var – does variable need to exist to be unset?

Naming #

Strive for meaningful, concrete, and descriptive names
Use a consistent naming scheme where possible
Avoid vague names, aim for precision/specificity
Avoid fluff words (e.g., fileObject, optionList)
Huffman principle: length of names can relate to lifetime of variable

Documentation #

The irrelevance of documentation has been largely exaggerated
Documentation can improve your design
Write documentation first
Separate interface and implementation comments
Comments should describe what is not obvious from the code. (They should not repeat the code.)

Design It Twice #

We often learn the flaws in our design only when we see it in action. Sometimes you can design it twice!

This is a surprisingly effective strategy, if not always feasible. But while it is not always possible in the large, it can be used for modules in a system.

Other common principles worth noting #

Make it run, make it right, make it fast – in that order
Don’t repeat yourself
Be consistent in style, format, interface structure, error handling, … (A practical not foolish consistency)
It’s easier to chew small pieces
Be conservative in what you send to others, be liberal in what you accept from others. (Postel’s law)
Write code to be read

Design Case Study #

Moving Off the Grid #

If you look closely at the description of the problem, and the rules, they make no mention of rows or columns. The only entities are living cells, neighborhoods, and dead cells in the neighborhood of live cells.

But the last of these can be derived from the other two. And the neighborhoods of a cell are static, specified by the geometry of the world.

The only state of the world we need to track is … wait for it …

THE SET OF LIVING CELLS

Two Key Operations #

neighbors to compute the neighbors of a cell
step to derive the next live cells from the current ones

neighbors is straightforward: perturb by 1,0,-1 but exclude both 0’s. In Python:

def neighbors_rect(location):
    x,y = location
    [((x + dx),(y + dy)) for dx in (-1,0,1) dy in (-1,0,1) if dx != 0 or dy !=0]

And in Clojure:

(defn neighbors-rect
  "Neighors of the cell [x y] in a rectangular grid"
  [[x y]]
  (for [dx [-1 0 1] dy [-1 0 1] :when (not= 0 dx dy)]
    [(+ x dx) (+ y dy)]))

But step is trickier:

Collect all the neighbors of live cells, with duplicates
Count how many time each cell is a neighbor (histogram)
Apply the rules (distinguishing current live from dead cells)

What arguments should step take?

neighbors – a function
rules – a (boolean) function or table
live cells – a set, e.g., {(0,1), (-2,1), (4,7), …}

def step(neighbors, rules, live_cells):
    "Step forward one generation, transforming set of live cells to the next one."
    frequencies = defaultdict(int)
    adjacencies = [neighbor for cell in live_cells for neighbor in neighbors(cell)]
    for neighbor in adjacencies:
        frequencies[neighbor] += 1
    return set([cell for cell,count in frequencies.items()
                if rules(count,cell in live_cells)])

(defn step
  "Step forward one generation, transforming set of live cells to the next one."
  [neighbors rules live-cells]
  (set (for [[location n-alive] (frequencies (mapcat neighbors live-cells))
             :when (rules n-alive (live-cells location))]
         location)))

It’s Just Geometry #

We can now apply the algorithm to a variety of different universes, different rules, and different steps.

typeclass Geometry a where
  neighbors : a -> List a

typeclass Status b where
  background : b
  isAlive : b -> Boolean
  isAlive status = status != background

type Cell a b where
  Cell : (Geometry a) -> (Status b) -> Cell a b

type Rule a b where
  Rule : (Cell a b -> List (Cell a b) -> b) -> Rule a b

typeclass (Geometry a, Status b) => Universe u where
  empty :: u
  assign :: Cell a b -> u -> u
  fromList :: List (Cell a b) -> u
  cellAt :: u -> a -> Cell a b
  living :: u -> List (Cell a b)

Hexagonal, toroidal, three-dimensional, …

All with the same code (up to one function!)

Speeding it Up #

Example: Hashlife by Bill Gosper

memoize configurations since many configurations recur frequently
use a quadtree to store the state in space and time e.g., 4x4 square stores 2x2 center, one generation ahead, 8x8 square stores 4x4 center, two generations ahead, and so forth